问题描述

给定二分图 $G=\langle X\cup Y, E\rangle$ 和权值函数 $w: E\to \mathbb R$（允许负权）。求匹配 $I\subseteq E$ 最大化

$$ cost(I)=\sum_{e\in I}w(e). $$

方法 1: 最大费用最大流

在二分图的网络流建模上，为边 $\langle u, v\rangle, u\in X, v\in Y$ 添加代价 $w(( u, v))$，为 $\langle s, u\rangle, u\in X$ 和 $\langle v, t\rangle, v\in Y$ 添加代价 $0$。

使用 SSP 求解最大费用的最大流，时间复杂度 $O(nmf)$，其中 $f=O(n)$ 且 $m=O(n^2)$，在稠密的二分图上，最坏是 $O(n^4)$ 的。

方法 2: KM 算法

KM 算法(Kuhn–Munkres Algorithm)可在 $O(n^3)$ 时间内解决二分图最大权匹配问题。

一类特殊二分图

在运行 KM 算法之前，假设图 $G$ 满足以下性质：

1. $G$ 是完全二分图。
2. $G$ 是平衡二分图。

对任意二分图，可以在左部或右部补充顶点满足条件 2.；可以加入 $0$ 或 $-\infty$ 的边满足条件 1.。所以该假设是不影响一般性的。

顶标和相等子图

顶标：

• 对于左部任意一点 $u\in X$，设置顶标 $lx_u$；
• 对于右部任意一点 $v\in Y$，设置顶标 $ly_v$。

要求：在算法运行的任意时刻，对任意边 $(u, v)\in E, u\in X, v\in Y$ 有

$$ lx_u+ly_v\ge w((u, v)). $$

相等子图 $G'=\langle V, E'\rangle$ 包含原图中的所有顶点，但仅包含原图中满足

$$ lx_u+ly_v=w((u, v)) $$

的边 $(u, v)$。可知相等子图由顶标序列决定。

相等子图的性质

Property 1: 若相等子图存在完美匹配，则该完美匹配的权就是顶标和 $\sum_{u\in X}lx_u+\sum_{v\in Y}ly_v$.

Proof of Property 1:

设完美匹配 $I$（恰有 $|X|=|Y|=n$ 条边）为 $\lbrace (u_i, v_i): 1\le i\le n\rbrace$，其中 $\lbrace u_i: 1\le i\le n\rbrace = X$，$\lbrace v_i: 1\le i\le n\rbrace=Y$ 且互不相同。由相等子图的性质知

$$ cost(I)=\sum_{i=1}^nw((u_i, v_i))=\sum_{i=1}^nlx_{u_i}+ly_{v_i}=\sum_{u\in X}lx_u+\sum_{v\in Y}ly_v. $$

Property 2: 若相等子图存在完美匹配，则该完美匹配就是原图的最大权完美匹配。

相等子图的性质

Proof of Property 2:

显然相等子图 $G'$ 的完美匹配 $I$ 是原图的完美匹配。对任意原图 $G$ 的完美匹配 $I'=\lbrace (u_i', v_i'): 1\le i\le n\rbrace$，有

$$ cost(I')=\sum_{i=1}^nw((u_i', v_i'))\le \sum_{i=1}^nlx_{u_i}+ly_{v_i}=cost(I). $$

故 $I$ 是 $G$ 的最大权匹配。

算法流程

只需求得具有完美匹配的相等子图即可。

Step 1: 赋予符合条件的初始顶标 $lx_u\gets\max_{v\in Y}\lbrace w((u, v))\rbrace$，$ly_v\gets0$。

Step 2: 从一个未匹配点开始在相等子图 $G'$ 中增广，即只经过 $lx_u+ly_v=w((u, v))$ 的边 $(u, v)$。

Step 3: 调整顶标，扩大相等子图 $G'$。重复 Step 2 和 Step 3 直至 $G'$ 包含恰 $n$ 条边。

调整顶标

为了扩大相等子图 $G'$，在 Step 2 经过的交错树中，让左部点顶标全部减少 $s$，让右部点顶标全部增加 $s(s> 0)$。

调整后，对于原图中的所有边，观察它的约束：（记 $u$ 和 $\hat u$ 分别为 $X$ 中在交错树和不在交错树的任意顶点，$v$ 和 $\hat v$ 同理）

• 边 $(u, v)$ 有 $lx'_u+ly'_v=lx_u-s+ly_v+s=lx_u+ly_v$，约束不变。
• 边 $(\hat u, \hat v)$ 有 $lx_{\hat u}'+ly_{\hat v}'=lx_{\hat u}+ly_{\hat v}$，约束不变。
• 边 $(u, \hat v)$ 要求有 $lx_u'+ly_{\hat v}'=lx_u-s+ly_{\hat v}\ge w((u, \hat v))$，有 $s\le lx_u+ly_{\hat v}-w((u, \hat v))$。
• 边 $(\hat u, v)$ 有 $lx_{\hat u}'+ly_v'=lx_{\hat u}+ly_v+s$，约束放松。

综上，选择 $\displaystyle s=\min_{u\in X, \hat v\in Y}\lbrace lx_u+ly_{\hat v}-w((u, \hat v))\rbrace$ 既可以满足约束，又可以使相应的 $\hat v$ 加入相等子图。

算法复杂性分析

至多扩增 $O(n)$ 次相等子图，每次进行增广(BFS)并维护顶标时间为 $O(n^2)$，总时间复杂度为 $O(n^3)$。

问题描述

图 $G=\langle V, E\rangle$ 的 $k$-支配集是点集的子集 $D_k\subseteq V$，使得去除 $V$ 中任意 $k-1$ 个顶点，剩余顶点或者在 $D_k$ 中，或者存在邻点在 $D_k$ 中。

最小支配集是 $k=1$ 时的该问题的特例。该问题是 NP-Hard 的。

[2] (Foerster, 2013) 中给出了一种近似率为 $\ln(\Delta+k)+1<\ln(\Delta)+1.7<\ln (n)+1.7$ 的贪心算法。

算法介绍

对于某个 $D\subseteq V$，定义某个顶点 $v\in V$ 在 $k$-支配集中的度 $d_k(v, D)$ 为

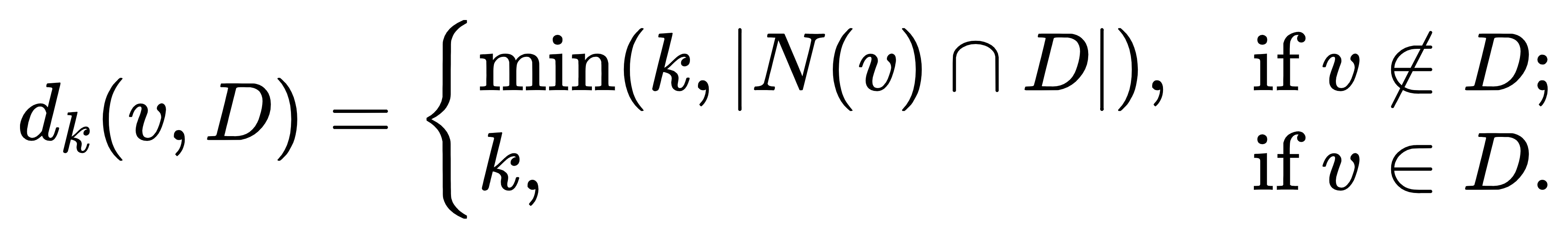
即表示 “还需在 $D$ 中补充 $k- d_k(v, D)$ 个 $v$ 的邻点才能使得 $D$ 在 $v$ 处成为 $k$-支配集合法”。

定义剩余代价 $a(G, D)$ 为

$$ a(G, D)=\sum_{v\in V}[k-d_k(v, D)]=nk-\sum_{v\in V}d_k(v, D). $$

则贪心算法则是依次迭代一系列 $D^{(0)}, D^{(1)}, \cdots, D^{(i)}$，每次加入一个顶点，使得 $a(G, D)$ 下降最快。

算法步骤

Step 1: 令 $D^{(0)}\gets\varnothing$，$i\gets 0$。

Step 2:

• 选择点 $v\in V\setminus D^{(i)}$ 使得 $a(G, D^{(i)})-a(G, D^{(i)}\cup \lbrace v\rbrace)$ 最大。
• 令 $D^{(i+1)}\gets D^{(i)}\cup \lbrace v\rbrace$，$i\gets i+1$。

Step 3: 重复 Step 2 直至 $a(G, D^{(i)})=0$，则此时 $D_k=D^{(i)}$ 是 $k$-支配集。

算法分析

该算法容易以 $O(n(n+m))$ 时间实现。为了分析近似率，我们使用以下数学结论：

Lemma: 若 $r\in \mathbb N, r>1$，且 $b_1, b_2, \cdots, b_s\in \mathbb N$ 满足

$$ b_v\ge \frac{1}{r}(B_s-B_{v-1}), \forall v\in\lbrace 1, 2, \cdots, s\rbrace $$

其中 $B_k=\sum_{i=1}^kb_i$ 为前缀和。

则有结论 $B_{\lambda}>B_s-r$，对于

$$ \lambda > \frac{\ln(\frac{B_s}{r})}{\ln(\frac{r}{r-1})}. $$

算法近似率

Theorem: 设 $r$ 是最小 $k$-支配集的代价（即 $OPT$），则该贪心算法近似率为

$$ \frac{\ln(\frac{nk}{r})}{r\ln(\frac{r}{r-1})}+1. $$

Corollary 1: 该算法近似率为 $\ln (\Delta + k)+1$。

Corollary 2: 该算法近似率为 $\ln(\Delta)+1.7<\ln(n)+1.7$。

推论证明

Proof for corollary 1: 用导数易证恒等式

$$ \frac{1}{\ln(\frac{r}{r-1})}\le r(1-\frac{1}{2r}), r\ge 0. $$

$$ \frac{\ln(\frac{nk}{r})}{r\ln(\frac{r}{r-1})}+1\le(1-\frac{1}{2r})\ln(\frac{nk}{r})+1<\ln(\frac{nk}{r})+1 $$

因为 $D_k$ 中的每个点为 $a(G, D_k)$ 从 $nk$ 变化到 $0$ 至多有 $\Delta+k$ 的贡献（$k$ 为自己，$1$ 为每个邻点），故有

$$ nk\le r(\Delta+k) \Leftrightarrow \frac{nk}{r}\le \Delta+k $$

于是 $\ln(\frac{nk}{r})+1\le \ln(\Delta+k)+1$ 也为该算法近似率。

推论证明

Proof for corollary 2: 当 $k>\Delta$，则唯一的 $k$-支配集是 $V$，贪心算法可得到最优解 $r=|V|$；若考虑 $k\le \Delta$，有

$$ \ln(\Delta+k)+1\le \ln(2\Delta)+1\le \ln(\Delta)+\ln 2 + 1 < \ln(\Delta)+1.7 $$

也为该算法近似率。

定理的证明

Theorem: 设 $r$ 是最小 $k$-支配集的代价（即 $OPT$），则该贪心算法近似率为

$$ \frac{\ln(\frac{nk}{r})}{r\ln(\frac{r}{r-1})}+1. $$

Proof: 设某个最小 $k$-支配集为 $D^*_k$。在从 $D^{(i-1)}$ 构造 $D^{(i)}$ 的过程中，若取 $D^{(i)}=D^{(i-1)}\cup D^*_k$，则 $a(G, D^{(i)})=0$。故在 $D^*_k\setminus D^{(i-1)}$ 中至少存在一个顶点 $u^{(i)}$ 使得 $a$ 下降 $a(G, D^{(i)})/|D^*_k|=a(G, D^{(i)})/r$。于是有

$$ a(G, D^{(i)})\le a(G, D^{(i-1)}\cup \lbrace u^i\rbrace)\le a(G, D^{(i-1)})\left(1-\frac{1}{r}\right) $$

定理的证明

取 $B_i=nk-a(G, D^{(i)})$，变形上式有

$$ B_i-B_{i-1}\ge\frac{1}{r}(nk-B_{i-1}). $$

令 $B_s=nk$，则由 Lemma，在

$$ \lambda > \frac{\ln(\frac{B_s}{r})}{\ln(\frac{r}{r-1})}=\frac{\ln(\frac{nk}{r})}{\ln(\frac{r}{r-1})} $$ 时有 $B_{\lambda}>B_s-r$，即 $a(G, D^{(\lambda)})<r$。再选至多 $r-1$ 个点即可使得 $a(G, D^{(\lambda+r-1)})=0$。

定理的证明

故最终答案可取

$$ |D_k|=\left\lfloor \frac{\ln(\frac{nk}{r})}{\ln(\frac{r}{r-1})}+1\right\rfloor+r-1=\left\lfloor \frac{\ln(\frac{nk}{r})}{\ln(\frac{r}{r-1})}\right\rfloor+r. $$

故近似率

$$ \alpha=\frac{|D_k|}{r}\le \frac{\ln(\frac{nk}{r})}{r\ln(\frac{r}{r-1})}+1 $$