概述

主要介绍最小直径生成树(Mininum diameter spanning tree, MDST)以及最小标签生成树(Mininum labeling spanning tree, MLST)的相关算法。

MDST 主要参考了文献 [1] (Hassin & Tamir, 1995) 和 [2] (Hakimi, 1964)；

MLST 主要参考了 [3] (Chang & Shing-Jiuan, 1997)。

最小直径生成树 - 定义

Def. 最小直径生成树(MDST)问题：对于非负权无向图 $G=\langle V, E\rangle$，寻找它的一棵生成树 $T^*$，使得对任意 $G$ 的生成树 $T$，有

$$ diam(T^*)\le diam (T) $$

其中 $diam(G')$ 是树 $G'$ 的直径，定义为

$$ \max_{u\in G'}\max_{v\in G'}dist(u, v). $$

• 应用场景：适用于各种要最小化单次最大传输距离（即最小化直径）的场景，区别于建设费用对应的 MST 问题。

绝对中心问题(Absolute 1 center problem, A1CP)

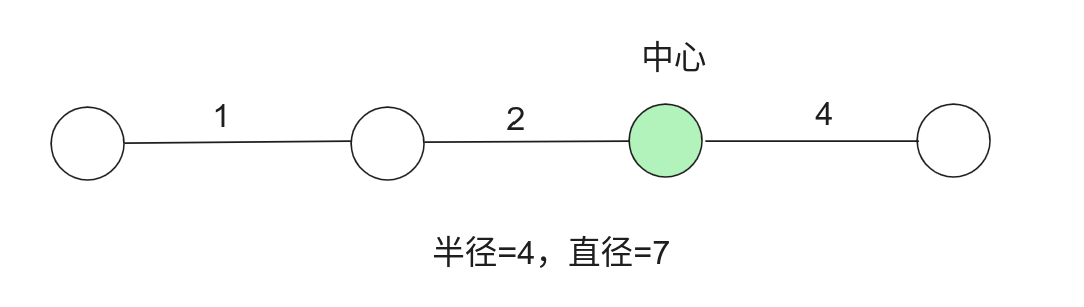
• 图的中心：离心率 $ecc(u)$ 最小的点 $u$。中心的离心率定义为图的半径 $rad(G)$。

  离心率 $ecc(u)$ 定义为 $u$ 到离它最远点的距离，即 $$ ecc(u)=\max_{v\in V}dist(u, v). $$

• 但是直径不一定是半径的两倍！

绝对中心问题(Absolute 1 center problem, A1CP)

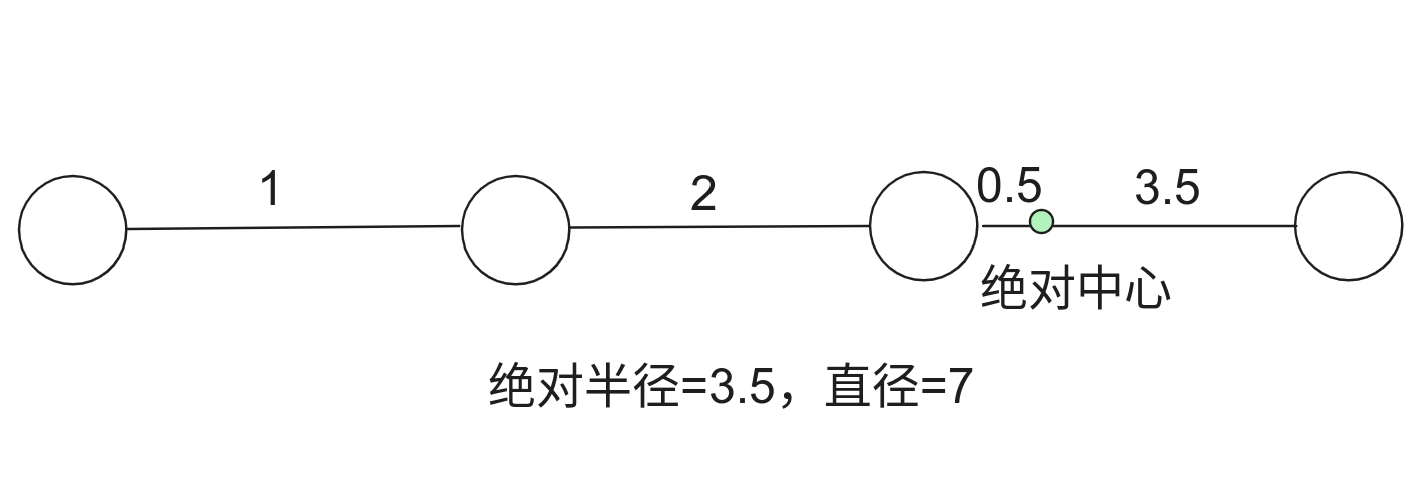
• 图的绝对中心：允许把边拆开，每条边可以认为有无数细分的点。把细分后的图记为 $G_A=\langle V_A, E\rangle$。定义图 $G$ 的绝对中心即为 $G_A$ 的中心，$G$ 的绝对半径即为 $G_A$ 的半径。容易发现：
  • $diam(G_A)=diam(G)$；
  • $G$ 的直径是绝对半径的两倍。

MDST 和 A1CP 等价

Theorem.(MDST 和 A1CP 的等价性) 图 $G$ 的绝对中心 $G^*$ 的一棵最短路径树 $T^*$ 是 $G$ 的 MDST。

Proof. 给定 $G$ 的任意一棵生成树 $T$，只需证明 $diam(T^*)\le diam(T)$。设 $T$ 的绝对中心是 $T^*$。

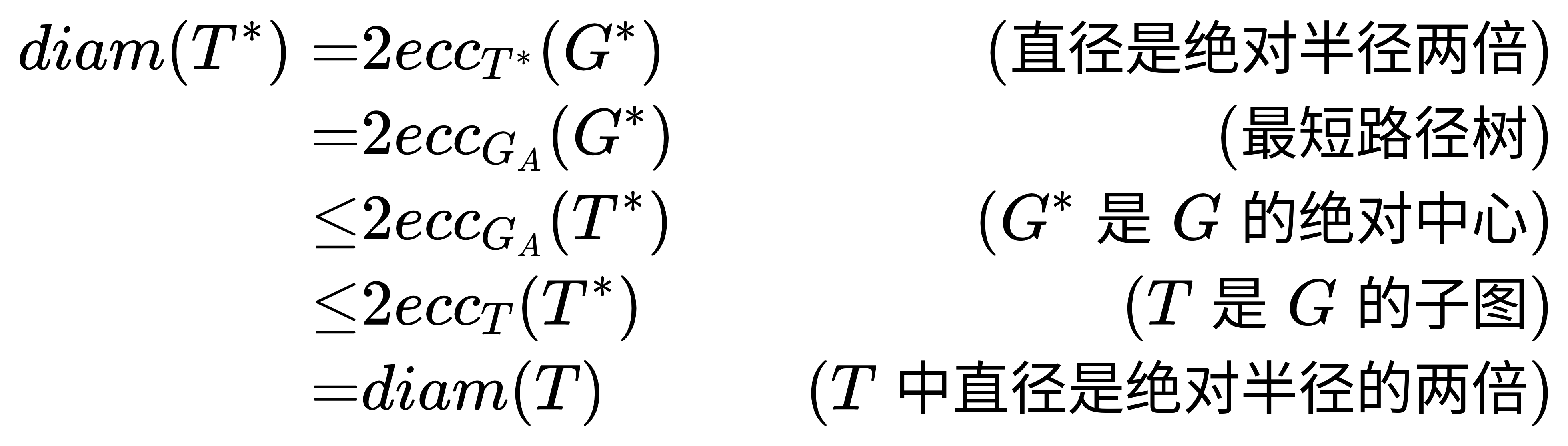
最短路径树可以在 $O(m+n\log n)$ 时间内求出。问题转化为寻找图的绝对中心。

寻找图的绝对中心

[2] (Hakimi, 1964) 给出了求图的绝对中心的方法。

绝对中心即 $G_A$ 上离心率最小的点 $u\in V_A$，而这样的 $u$ 一定在某条边上。

故可以分别考虑每条边上离心率最小的点 $G^*(e)$，称为 $e$-边绝对中心。最后 $G^*$ 就是 $\arg \min_{G^*(e)}ecc(G^*(e))$。

寻找 $e$-边绝对中心

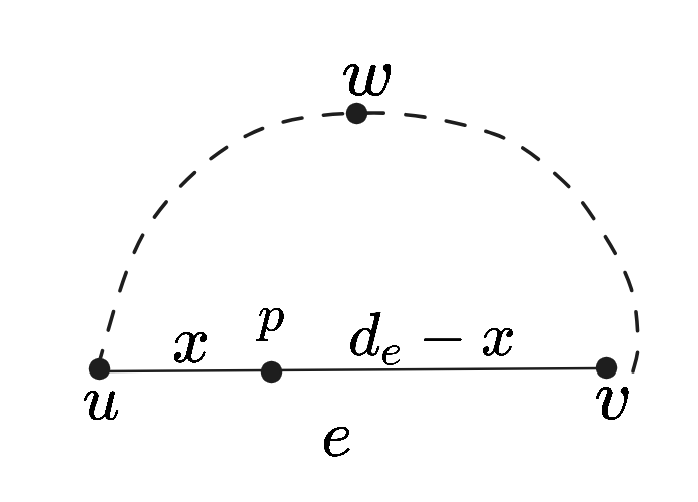
对边 $e=(u, v)$，考虑离 $u$ 距离为 $x$ 的内点 $p$，它离 $V$ 中每个顶点 $w$ 的最小距离为

$$ dist(p, w)=\min(x+dist(u, w), -x+d_e+dist(v, w)) $$

寻找 $e$-边绝对中心

以 $dist(p, w)$ 和 $x$ 为坐标系，描述了一个函数关系。

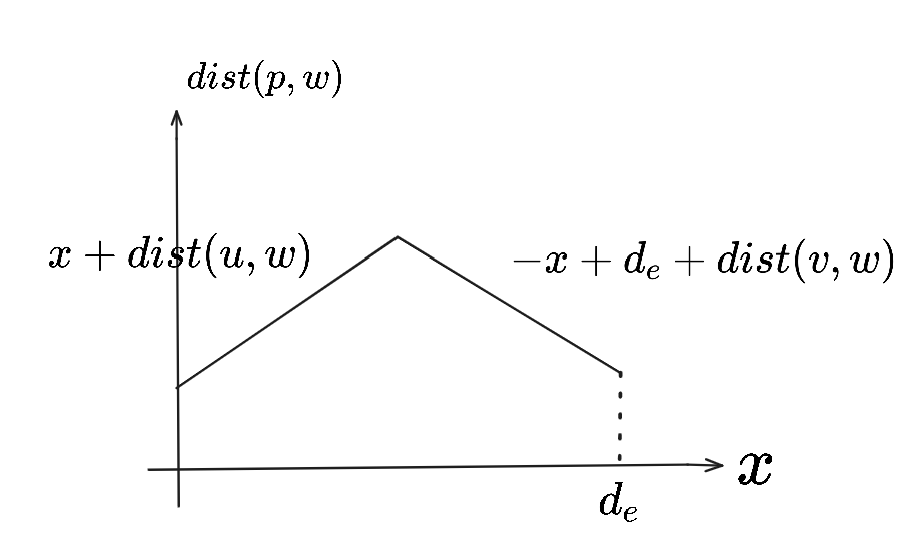
寻找 $e$-边绝对中心

把全部的 $w$ 遍历一遍，取最大值得到 $ecc$ 对应的函数。

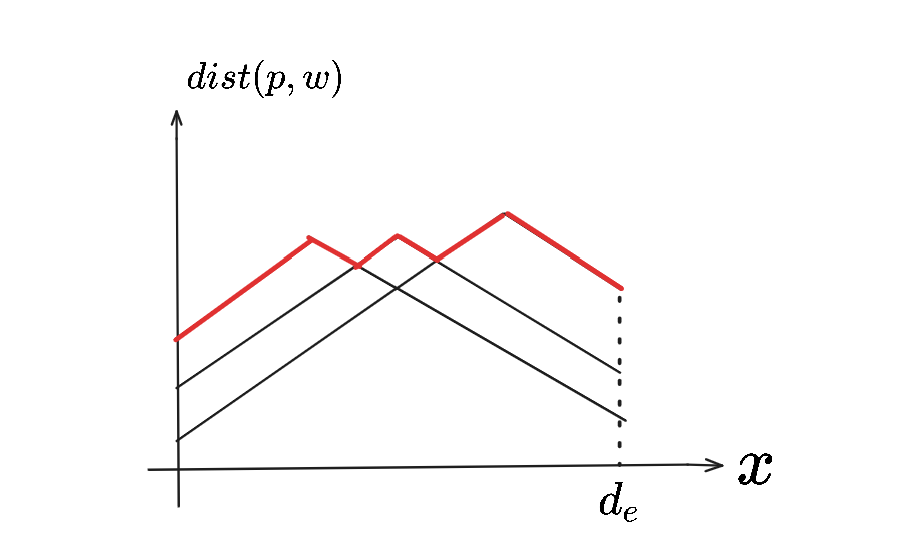
容易线性 $O(n)$ 得到函数最小值，从而得到 $e$-边绝对中心。

对每条边考虑，得到 $G$ 的绝对中心，时间复杂度 $O(nm)$。

算法瓶颈在于计算 ASAP。总时间复杂度为 $O(nm+n^2\log n)$。

总结

我们可以在 $O(nm+n^2\log n)$ 时间内计算 A1CP，然后用 $O(m+n\log n)$ 时间内求出绝对中心的最短路径树，即最小直径生成树。总时间复杂度为 $O(nm+n^2\log n)$。

最小标签生成树 - 定义

Def. 最小标签生成树(MLST)问题：给定图 $G=\langle V, E\rangle$ 和标签函数 $L: e\to S_L$，寻找 $G$ 的一棵生成树 $T$，最小化 $|L(E(T))|$，即最小化 $T$ 使用了的标签数量。

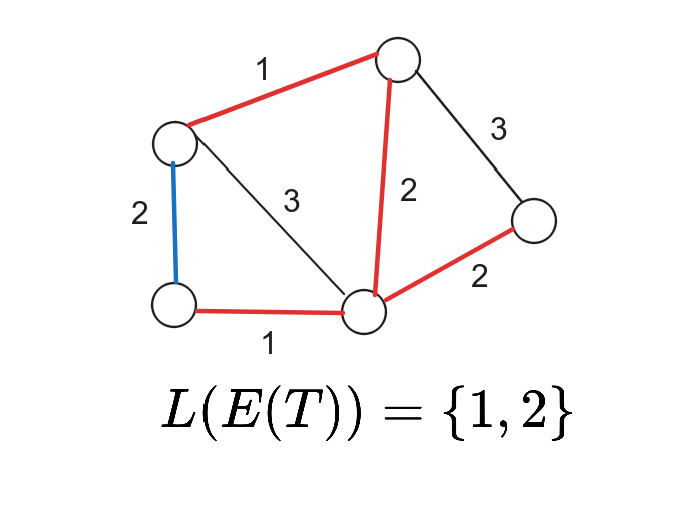
• 应用场景：比如，在信息传递中，边代表传播介质（有光纤、电磁波、电话线、电缆等）。建设成本定义为使用的介质种类，这时最小化成本就是寻找 MLST。

MLST is NP-hard

通过将最小覆盖问题归约到 MLST 的判定版本 BLST，得到 BLST 是 NP-Complete，从而 MLST 是 NP-hard。

Def. Bounded 标签生成树(BLST)问题：给定图 $G=\langle V, E\rangle$ 和 上界 $W$，是否存在 $|L(E(T))| \le W$ 的生成树 $T$。

显然 BLST 是 NP 的，只需证明它是 NP-hard，从而是 NP-Complete 的。

Def. 最小覆盖问题：给定集合 $S=\lbrace a_1, a_2, \cdots, a_n\rbrace$ 与上界 $W$，和 $m$ 个 $S$ 的子集 $C_1, C_2, \cdots, C_m\subseteq S$，是否存在 $\le W$ 个 $C_i$ 能够覆盖 $S$。

归约

对于给定的最小覆盖问题 $\langle S, W, C_1, C_2, \cdots, C_m\rangle$，建图如下：

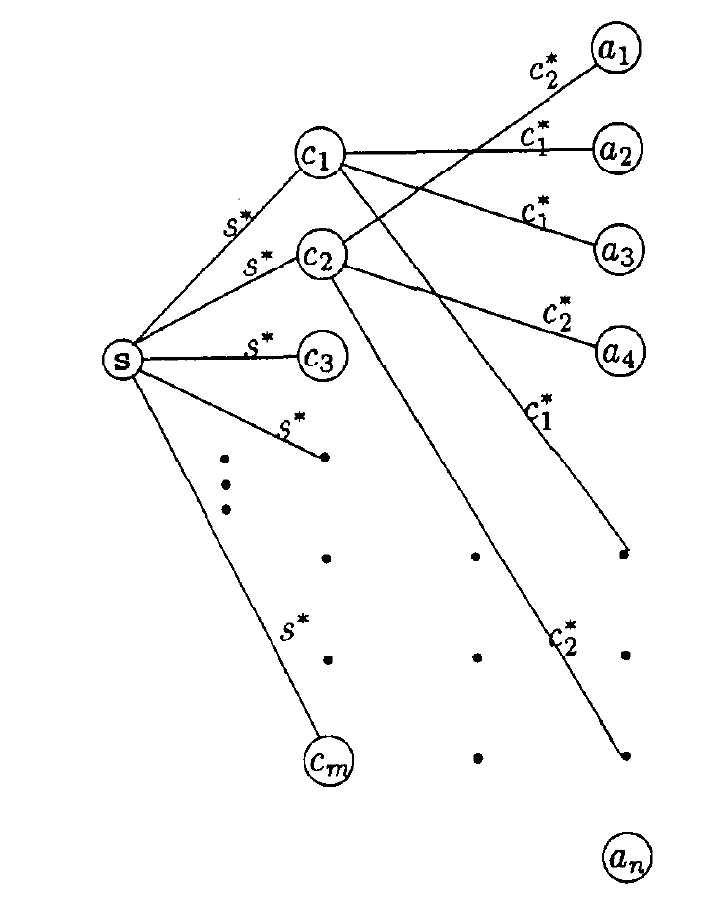
图片来源：[3] (Chang & Shing-Jiuan, 1997)

若存在该图存在 $(W+1)$ BLST，则原问题存在 $W$ 最小覆盖。该归约显然是 poly 的。因为最小覆盖是 NP-Complete 的，故 BLST 也是 NP-Complete 的。从而 MLST 是 NP-hard 的。

MLST 的启发式算法

Edge Replacement Algorithm:

• 任选一棵生成树 $T$。
• 尝试每条非树边，判断将这条边替代合法树边得到 $T'$ 后使用的标签数能否减小，若可以减小则替代。

时间复杂度为 $O(mn)$。

Maximum Vertex Covering Algorithm:

• 当图不连通时，在还未选过的标签中，选取加入后连通分支数目减少最多的标签，依次反复，直到图连通。

时间复杂度为 $O(lmn)$，$l$ 为标签总数。

MLST 的精确算法 - A*

将“每次搜索一个新的标签”的搜索算法改造成 A*。

$$ f(x)=g(x)+h(x) $$

• $g(x)$ 是已经使用了的标签数量；
• $h(x)$ 计算方法是：
  • 首先得到由已选定的标签构成的连通块个数 $t$。则还需要 $need=t-1$ 条树边；
  • 然后设还未选过的标签对应的边数由高到低为 $e_1, e_2, \cdots, e_{l'}$；
  • 设置 $h(x)$ 为最小的 $j$ 使得 $\sum_{i=1}^je_i\ge need$.

可以知道 $h(x)$ 一定 $\le$ 真实值 $h^*(x)$，保证了 A* 的正确性。