简介

• 给定 $N$ 盏灯，位置分别为 $x_1, x_2, \cdots, x_N$，满足 $1\le x_i\le V$。
• 再给定 $Q$ 个询问 $d_i, (1\le d_i\le V)$，对每个询问求出最小的 $v\in\lbrace 1, 2, \cdots, n\rbrace$ 使得在 $x_v+d_i$ 处存在另一盏灯。
• 设 $N$，$Q$，$V$ 为同一量级。

分析

该问题并非是难问题，存在朴素的 $O(QN)$ 的实现。但若对于编号的“最小”可以进行一定的宽松，可以获得复杂度更低的算法。

考虑近似率为 $\alpha$ 的算法，即允许输出的答案 $v'$ 满足 $v\le v'\le \alpha v$，此时可以使用“区间划分”的思想对问题进行简化。

下界的确定

• 假若我们已确保对询问 $d_i$，对任意 $v'< k$，$v'$ 均不满足 $x_{v'}+d_i$ 处有灯，则最优解有下界 $k$。
• 此时，若编号在 $v\in [k,\lfloor \alpha k\rfloor]\cap \mathbb Z$ 区间内的点有满足条件的，则最优解满足 $v\in [k, \lfloor \alpha k\rfloor]$，从而 $v'=\lfloor \alpha k\rfloor$ 是原问题的一个满足近似率为 $\alpha$ 的解。
• 否则，则证明了所有编号在 $[1,\lfloor \alpha k\rfloor]$ 中的点都不满足条件，最优解有新的下界 $\lfloor \alpha k\rfloor+1$.

下界的确定

若不考虑下取整，重复 $t$ 次上述步骤，下界序列为：

• $low_1=1$;
• $low_2=\alpha + 1$;
• $low_3=\alpha(\alpha + 1) + 1$;
• $\cdots$;
• $low_t=\sum_{i=0}^{t-1}\alpha^i=\frac{\alpha^t-1}{\alpha-1}$.

令 $low_t\le n$，有 $t\le\log_\alpha(\alpha(n-1)+1)$，故 $t=\Theta(\log_\alpha n)$. 于是至多进行 $\Theta(\log_\alpha n)$ 次该操作。

询问的整体处理

于是，问题转化为了，对至多 $\Theta(\log_\alpha n)$ 段形如 $[L, R]$ 的编号区间，对每个询问 $d_i(1\le i\le Q)$，判断是否存在 $v\in [L, R]$ 使得 $x_v+d_i$ 存在另一盏灯。

事实上，可以对所有 $d_i$ 一起处理：构造两个序列 $X_i$ 和 $Y_i$：

• $X_i=1$ 当且仅当存在 $v\in [L, R]$, $x_v=i$；否则为 $0$。
• $Y_i=1$ 当且仅当存在 $v\in [1, N]$，$x_v=i$；否则为 $0$。
• "存在多少对 $(x, y)$ 满足 $x\in [L, R], y\in [1, n], s.t. x+d=y$" 也可以形成一个序列 $Z_d$，计算方法为

$$ Z_d=\sum_{1\le i, j\le V, j-i=d}X_iY_j. $$

$Z_d$ 的快速计算

可以将 $X$ 序列翻转，变成加法卷积：

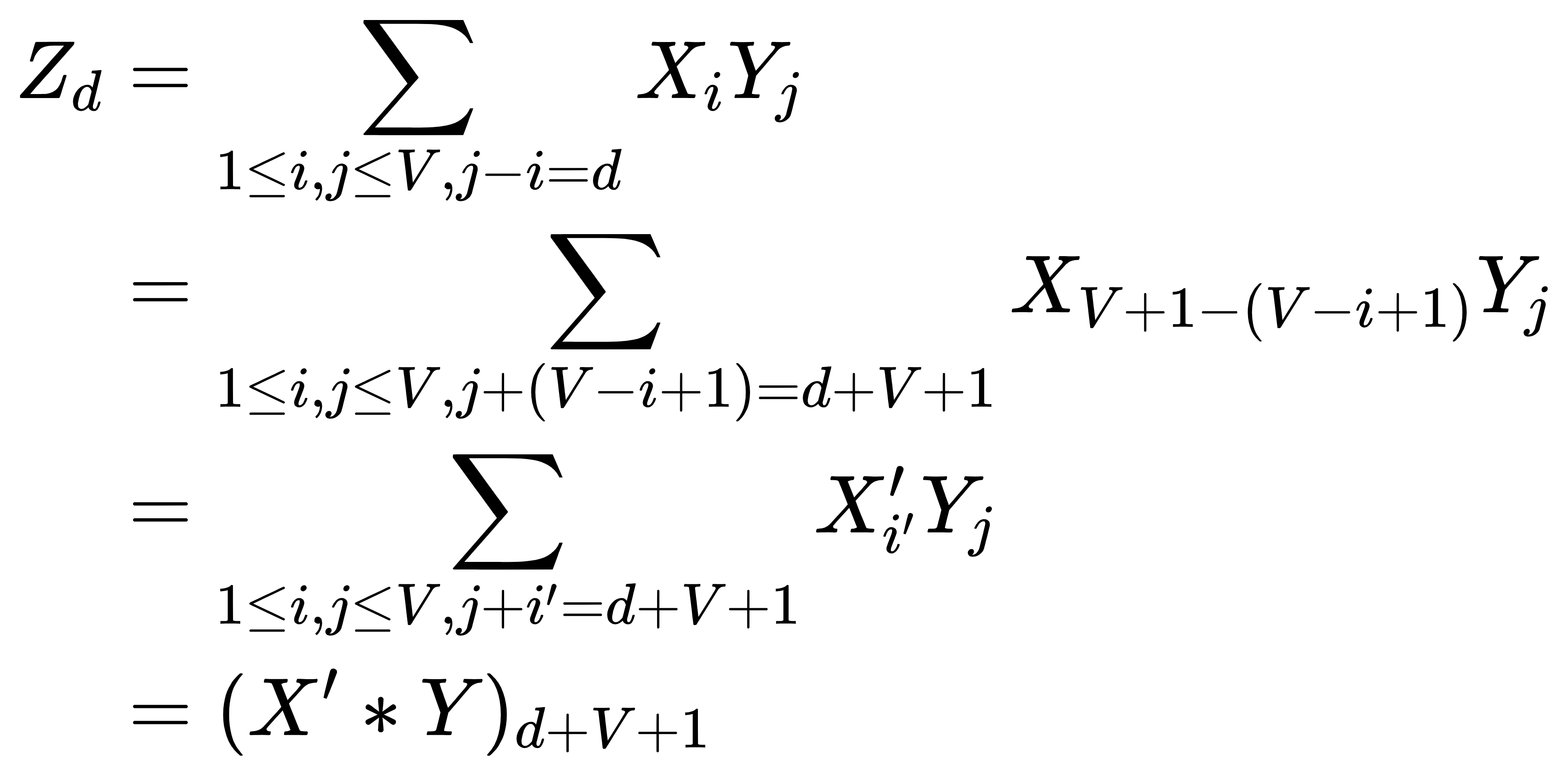
其中，$i'=V-i+1, X_k' = X_{V+1-k}$。

而加法卷积可以使用快速傅里叶算法在 $\Theta(V\log V)$ 时间内计算。之后对每个询问 $d_i$，只需判断 $Z_{d_i}$ 是否为 $0$ 即可。

算法分析

最朴素的算法为 $O(QN)$；

该算法在近似率为 $\alpha$ 的情况下，共至多运行 $O(\log_\alpha N)$ 轮区间 $[L, R]$ 的查询，单次复杂度为 $O(V\log V+Q)$，故总复杂度为 $O((V\log V+Q)\log_\alpha N)$。

问题描述

• 给定 $m$ 个集合 $S_1, S_2, \cdots, S_m$ 和 $k$，要求选定其中 $k$ 个 $S_{p_1}, S_{p_2}, \cdots, S_{p_k}$，最大化 $S_{p_1}\cup S_{p_2}\cup\cdots, S_{p_k}$。
• 该问题为 NPC。

贪心算法

对以下步骤进行 $k$ 轮：

• 第 $i$ 轮，每次选择集合 $S_{p_i}$ 最大化新增的并集大小。

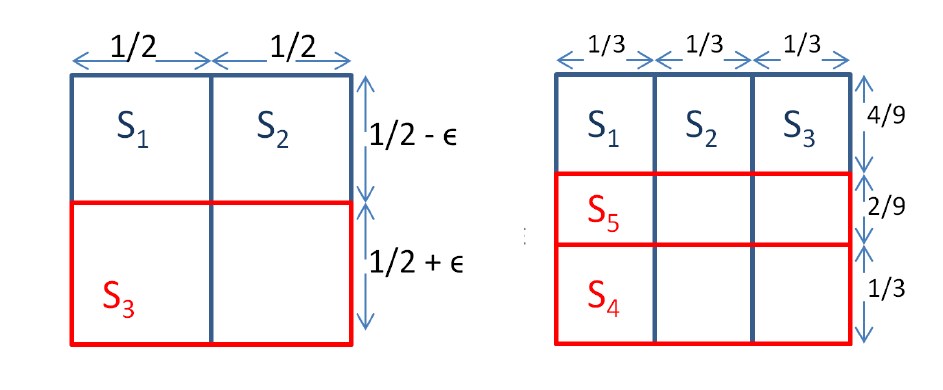
如上图，可构造出近似率不高于 $\displaystyle 1-(1-\frac{1}{k})^k$ 的样例。

• (方便起见，此处近似率未取倒数，定义为 $\alpha=\text{Now-Sol}/OPT$)

近似率证明

Theorem 1: 该贪心算法的近似率恰为 $\displaystyle(1-(1-\frac{1}{k})^k)$，故该近似率估计是紧的。

要证明 Theorem 1，先证明引理

Lemma: 设贪心算法选择出前 $i-1$ 个集合为 $S_{p_1}, S_{p_2}, \cdots, S_{p_{i-1}}$，它们覆盖了 $l$ 个元素，则第 $i$ 轮选择的 $A_i$ 会覆盖至少

$$ \frac{1}{k}(OPT-l) $$ 个新元素，$OPT$ 为最优解。

Proof: 假设该轮贪心算法可以直接取走 $k$ 个集合，则可以立即取到 $OPT$ 个元素，获得至少 $OPT-l$ 个新元素。故这 $k$ 个中至少有一个集合有至少 $\frac{1}{k}(OPT-l)$ 个新元素。

近似率证明

Theorem 1: 该贪心算法的近似率恰为 $\displaystyle(1-(1-\frac{1}{k})^k)$，故该近似率估计是紧的。

Proof:

设第 $i$ 轮共取了 $f_i$ 个元素，则有 $f_0=0$，且

$$ f_i\ge f_{i-1}+\frac{1}{k}(OPT-f_{i-1})=\frac{1}{k}OPT+(1-\frac{1}{k})f_{i-1}. $$

解递推式有

$$ f_{i}\ge OPT+(1-\frac{1}{k})^k(f_0-OPT)=OPT\cdot (1-(1-\frac{1}{k})^k). $$

故

近似率证明

$$ \frac{f_i}{OPT}\ge 1-(1-\frac{1}{k})^k $$ 近似率为 $\displaystyle \alpha=1-(1-\frac{1}{k})^k$.

总结

Theorem 2: 在某些复杂度假设下，不存在有更优近似率的多项式复杂度算法。