Introduction

在某些松弛修正算法的分析中，欧拉图经常出现。本次报告选择了以下两个主题：

• 在线斯坦纳树的贪心算法
• Metric TSP 的启发式算法。包括 MST Heuristic 算法和改进的 Christofides 算法。

Description

• 提前给定：连通无向图 $G=\langle V, E\rangle$，非负权。
• 在线回答：依次给定 $t_1, t_2, \cdots, t_k$，在给定 $t_i(1\le i\le k)$ 后将其增量连接到 $i-1$ 时构造的子图。要求使得在 $k$ 次迭代后的子图边权和尽量小。

容易发现是最小斯坦纳树问题的在线版本。

Assumptions

不失一般性地假设：

1. 图 $G=\langle V, E\rangle$ 是完全图。
2. 图 $G$ 中边权满足三角不等式(metric)。

其中假设 1. 不失一般性，因为非完全图可补充无穷大的边；

假设 2. 不失一般性，是由算法决定的。

A greedy method

1. 一开始选择空树 $T_0$。
2. 对于 $t_1$，令 $T_1=T_0$ 也为空树。
3. 对于 $t_j(2\le j\le k)$，选择最小的边 $( t_i, t_j), i<j$ 加入 $T_{j-1}$ 中得到 $T_j$。
4. $T=T_k$ 即为最终解，$cost(\text{GREEDY})=cost(T_k)$。

(picture from [1])

直观地理解：每次将 $t_i$ 以最小代价“贴”到现存的树上去。

Instances

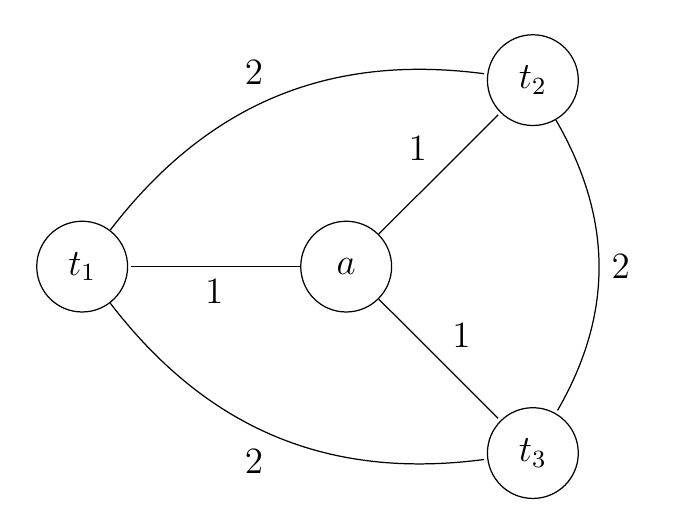
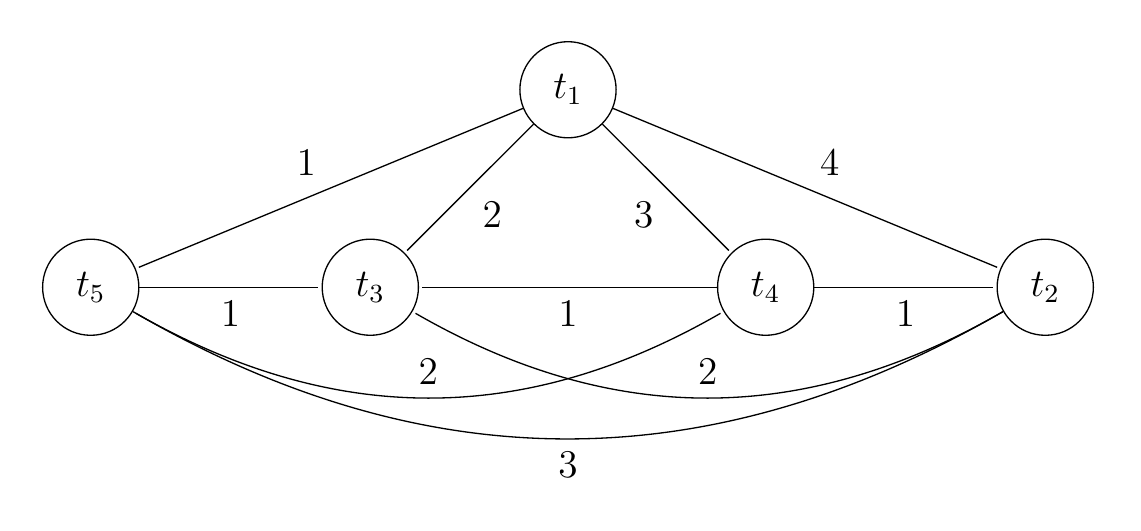
其中对于样例右，最优解为 $4$，但贪心算法求得的解为 $8$。

Theorem: 该贪心算法最坏 performance ratio 为 $\Omega(\log k)$。

Theorem: 对任何在线斯坦纳树的算法，最坏情况下的 performance ratio 都是 $\Omega(\log k)$。

Algorithm analysis

Theorem: 该贪心算法的 performance ratio $< 2\ln k$，从而该贪心算法渐进最优。

Proof: 要证该定理，只需证明

Lemma: 对任意 $p=1, 2, \cdots, k-1$，该贪心算法选择的 $T$ 中第 $p$ 大的边权不超过 $2OPT/p$，其中 $OPT$ 是全局最优解。

Algorithm analysis(cont'd)

若该引理成立，则设 $T$ 中所有边按边权从大到小排为 $e_1, e_2, \cdots, e_{k-1}$，有

$$ e_p\le \frac{2OPT}{p}, p=1, 2, \cdots, k-1. $$

故而

$$ cost(\text{GREEDY})=\sum_{p=1}^{k-1} e_p\le \sum_{p=1}^{k-1}\frac{2OPT}{p}<2OPT\ln k. $$

从而

$$ \alpha=\frac{cost(\text{GREEDY})}{OPT}<2\ln k. $$

Proof of the Lemma

Lemma: 对任意 $p=1, 2, \cdots, k-1$，该贪心算法选择的 $T$ 中第 $p$ 大的边权不超过 $2OPT/p$，其中 $OPT$ 是全局最优解。

Proof:

1. 设 $T^*$ 是全局最优解对应的斯坦纳树，$OPT=cost(T^*)$。
2. 将 $T^*$ 所有边都复制一份，可以得到一个所有顶点都为偶点的图 $H$，故其具有欧拉回路 $C$，且 $cost(C)=2OPT$。

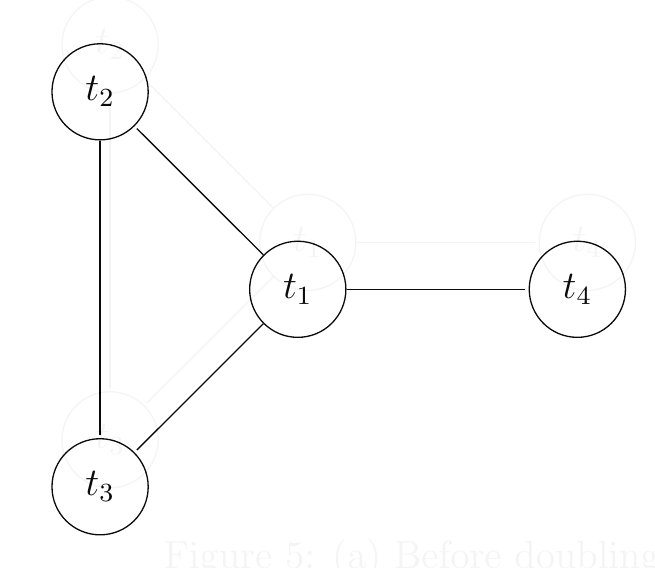
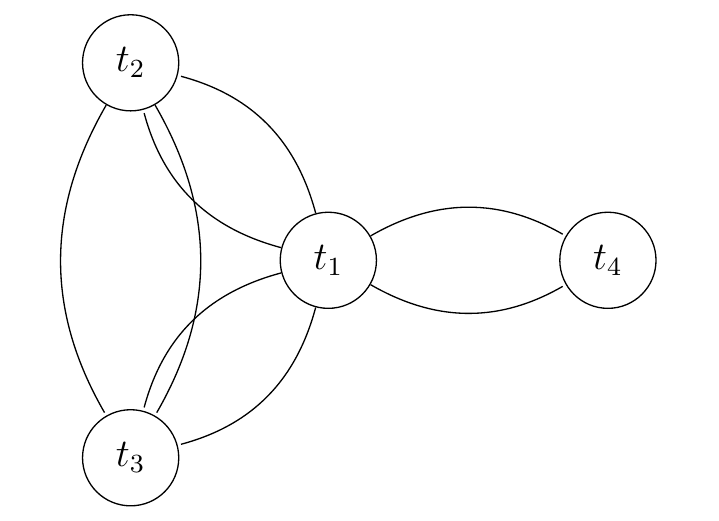
3. 对给定的 $p\in \lbrace 1, 2, \cdots, k-1\rbrace$:

• 定义一个点 $t_j(j>1)$ 的连通代价为在 GREEDY 中将 $t_j$ 与 $T_{j-1}$ 合并得到 $T_{j}$ 的新增代价（即权值最小的 $(t_i, t_j), i<j$ 边）。
• 设连通代价最高的 $p$ 个依次为 $s_1, s_2, \cdots, s_{p}\subseteq \lbrace t_2, t_3, \cdots, t_k\rbrace$。不妨设连通代价 $w(s_j)$ 依次递减。 则该命题只需证明：$w(t_k)\le 2OPT/i$。

4. 由于 $C$ 经过 $t_1, t_2, \cdots, t_k$ 中的每个点，故也经过 $s_1, s_2, \cdots, s_p$。可以将欧拉回路 $C$ 进行“裁剪”得到一个 $s_1, s_2, \cdots, s_p$ 的哈密尔顿圈 $C'$：由于图满足三角不等式，可将路径用其端点关联的边直接替代，且 $cost(C')\le cost(C)=2OPT$。

5. $C'$ 中含有 $p$ 条边，故其最小边 $(s_i, s_j)$ 满足 $w((s_i, s_j))\le cost(C')/p\le 2OPT/p$.

6. 不妨设 $i<j$，则 $s_j$ 的连通代价不超过 $w((s_i,s_j))\le 2OPT/p$，从而命题得证。

Heuristic

可以发现采用的是“构造偶点图 $\to$ 得到欧拉回路 $\to$ 得到哈密尔顿圈”的分析方法。在 TSP 的近似算法中，可以再次发现这种想法的应用。

Reason of the 2nd. assumption

若某图不满足三角不等式，可现在其最短路径闭包上使用上述算法，并映射回原图。

Description

Definition(Metric TSP): 给定非负权无向连通图 $G=\langle V, E\rangle$，满足三角不等式，求最小化 $cost(H)$ 的哈密尔顿圈 $H$。

Continue the same heuristic

在在线斯坦纳树的算法分析中直接出现了哈密尔顿圈！

是否同样可以用欧拉回路来得到一个不错的 bound 呢？

MST Heuristic: 注意到，对于 $G=\langle V, E\rangle$ 的最小生成树 $T$，有

$$ cost(T)\le cost(H). $$

其中 $H$ 为图 $T$ 任意哈密尔顿圈。

MST Heuristic

算法流程：

1. 求出 $G$ 的一棵最小生成树，可知 $cost(T)\le cost(H)=OPT$，$OPT$ 为问题最优解。
2. 将 $T$ 中每条边复制一遍，得到全是偶点的图，可得经过所有点的欧拉回路 $C$，有 $cost(C)=2cost(T)\le 2OPT$。
3. 裁剪 $C$ 得到哈密尔顿圈 $H'$，有 $cost(H')\le cost(C)\le 2OPT$。

显然得到了近似率

$$ \alpha=\frac{cost(C)}{OPT}\le 2 $$

的算法。容易在 $O(n^2)$ 内实现。

Christofides's Algorithm

在最小生成树 $T$ 的基础上，无需将其所有边都复制一遍来得到欧拉回路。Christofides 算法使用了更好的松弛：

算法流程：

1. 仍求得一棵最小生成树 $T$，$cost(T)\le OPT$。
2. 子图 $T$ 中 $\deg_T(u)$ 为奇数的点构成集合 $V_{odd}$，有 $|V_{odd}|$ 为偶数。
3. 因为 $V_{odd}$ 的导出子图为完全图，故其存在完美匹配，记其最小权的为 $M$。
4. $\langle V, E[T]\cup E[M]\rangle$（允许重边）全为偶点，存在欧拉回路 $C$。
5. 裁剪 $C$ 得到哈密尔顿圈 $H'$。

Christofides's Algorithm - Analysis

对于图 $\langle V, E[T]\cup E[M]\rangle$，其 $E[T]$ 的部分显然有 $cost(T)\le OPT$。只需考虑 $cost(M)$ 和 $OPT$ 的大小关系。

Lemma: 对于偶阶子图 $G'\subseteq_{g} G$，其最小权完美匹配 $M$ 满足 $cost(M)\le OPT/2$。

Proof:

1. 可将 OPT 对应的哈密尔顿圈 $H$ 裁剪至 $V[G']$ 上得到 $H[G']$，由 metric 可知 $cost(H[G'])\le OPT$。
2. $H[G‘]$ 含有偶数条边，交替构成两个匹配 $M_1, M_2$，有 $cost(M_1)+cost(M_2)\le cost(H[H'])\le OPT$。
3. 不妨设较小的那个是 $M_1$，有 $M\le M_1\le OPT/2$。

Christofides's Algorithm - Analysis (cont'd)

由 Lemma 可得，最后求得的 $H'$ 满足

$$ cost(H')\le cost(C)=cost(T)+cost(M)\le OPT+OPT/2=3OPT/2 $$

故近似率 $\alpha \le 3/2$。

算法瓶颈在于一般图最大权匹配，时间复杂度 $O(n^3)$。