简介

未加说明的定义见 [1] (Sommer, 2014)。

Distance oracle 是一种距离 stretch，空间 space 和单次查询时间 query time 的权衡的艺术。

DO 的历史发现

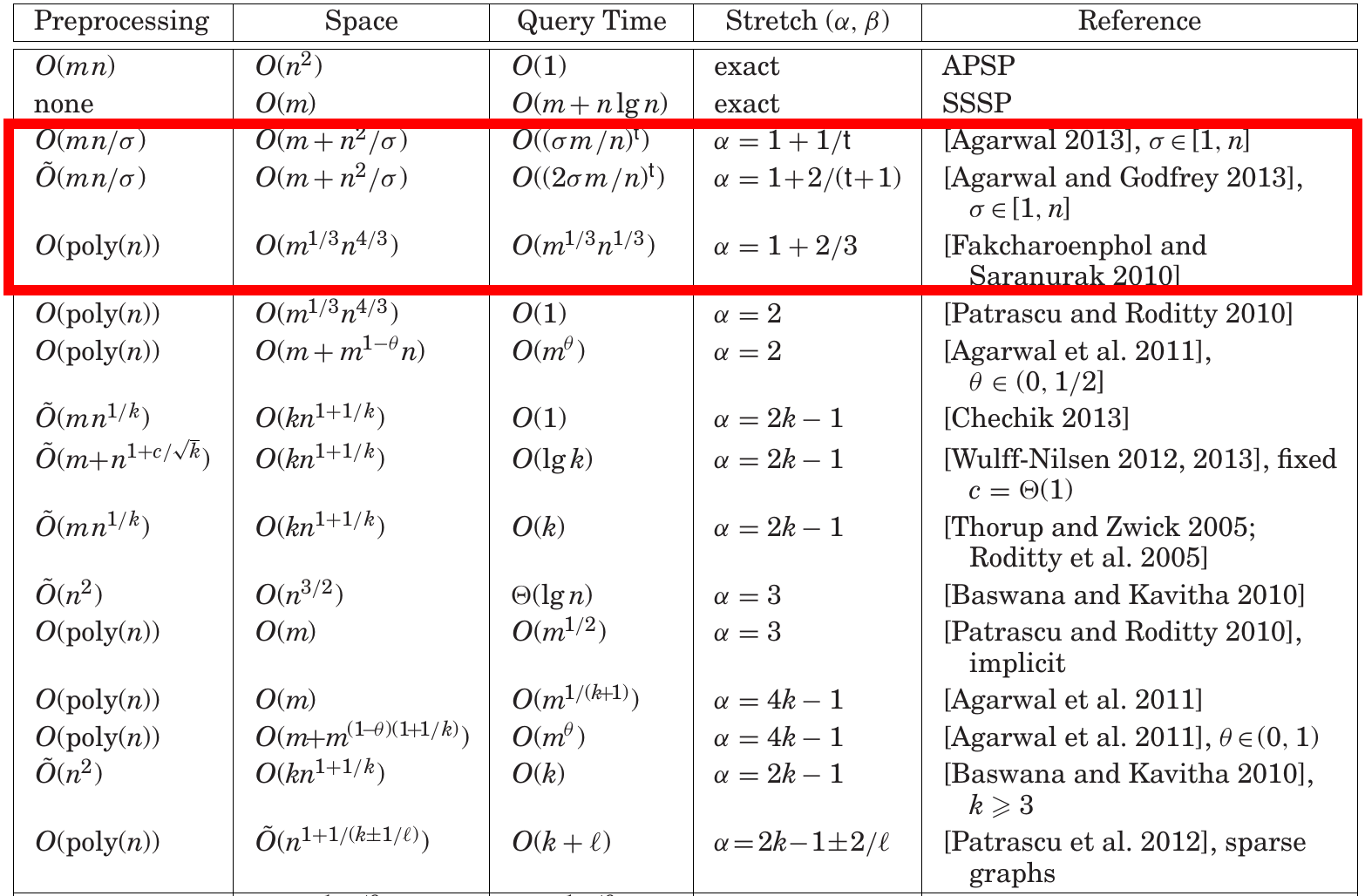
论文贡献

[2] (Agarwal, 2014) 提供了三种满足 stretch $\alpha\in(1, 2]$ 的 DO。

我们主要讨论第一个成果：

Result: 对于平均度为 $\mu=2m/n$ 的图，对任意 $1\le \alpha \le n$，存在 stretch 为 $O(1+1/k)$，询问时间 $T=O((\alpha \mu)^k)$，空间为 $S=O(m+n^2/\alpha)$ 的 DO。

约束方程：

$$ S\times T^{1/k}=O(n^2) $$

主要思想

• 经典的 landmark 法：选一个 landmark 集 $L$，对所有点存储到它们的距离。
• 合理地选择多级 landmark，使得估计距离 $\delta(s, t)$ 和实际距离的误差尽量小。
• 和 Agarwal 的之前的成果相比：创新性地使用了双向方法来处理询问。
• 正是由于双向的优化，在不影响 space 和 construction time 的前提下，query time 得到了大幅优化：

图的结构性预处理 - degree bounded

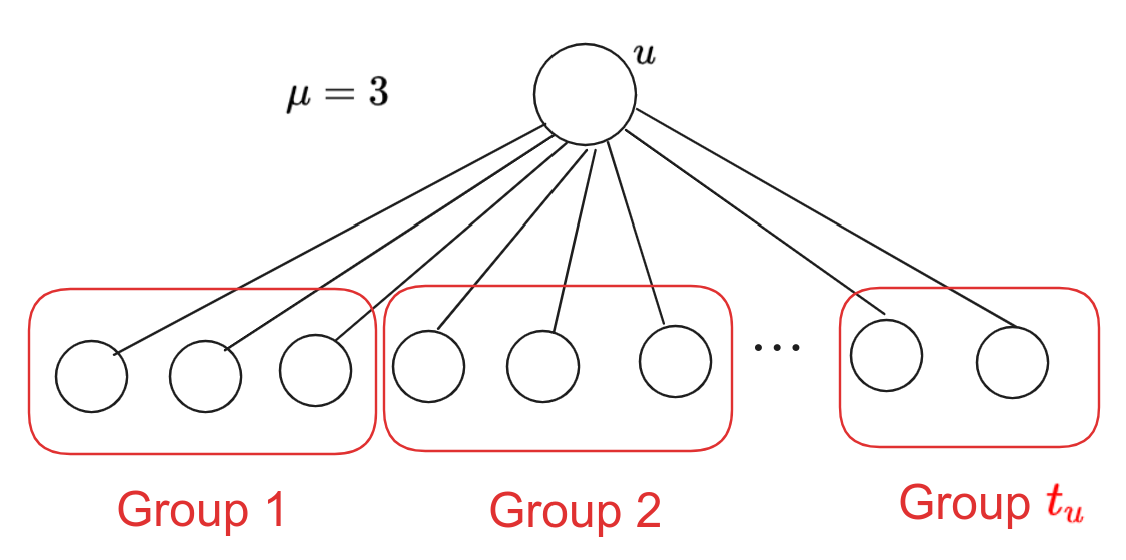
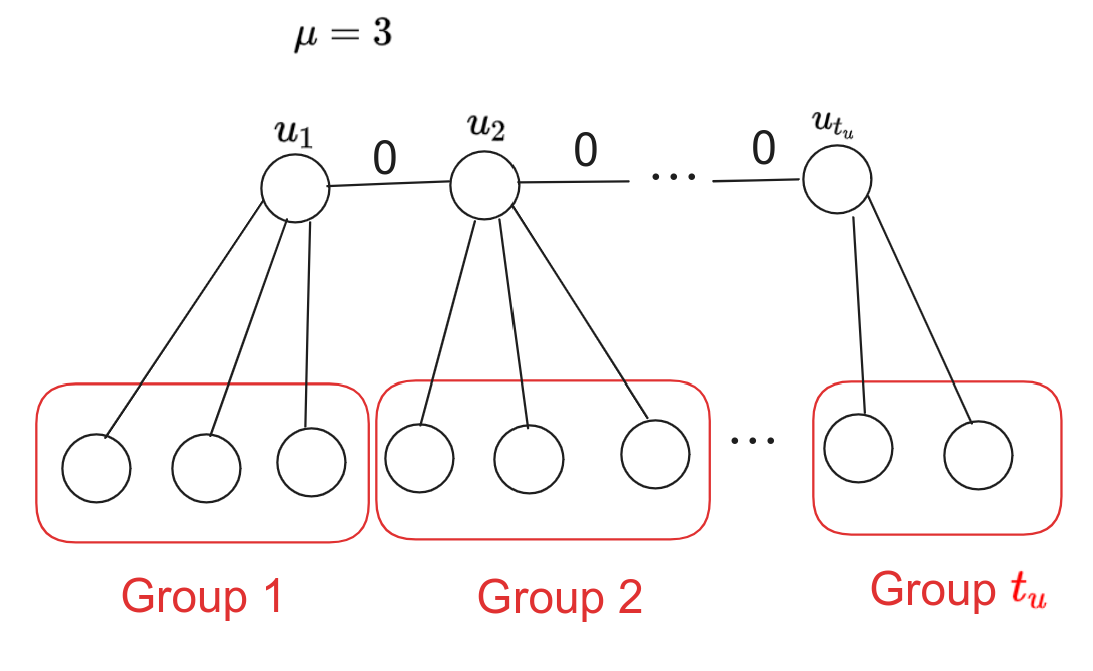
Theorem: 任何 $n$ 点 $m$ 边的图都可以转化为不超过 $2n$ 点，所有点度数不超过 $\lceil \mu + 2\rceil$ 的图。（$\mu$ 是原图的平均度数，为 $2m/n$）。

Construction: 在新图 $G'$ 中，将所有点 $u$ 转化为 $t_u=\lceil \deg(u)/\mu\rceil$ 个点 $u_1, u_2, \cdots, u_{t_u}$。将原图中 $u$ 的邻点分成 $t_u$ 组，每组不超过 $\mu$ 个，在新图中连到这 $t_u$ 个点上。最后将这 $t_u$ 个点在新图中用零边连成链。

基础定义

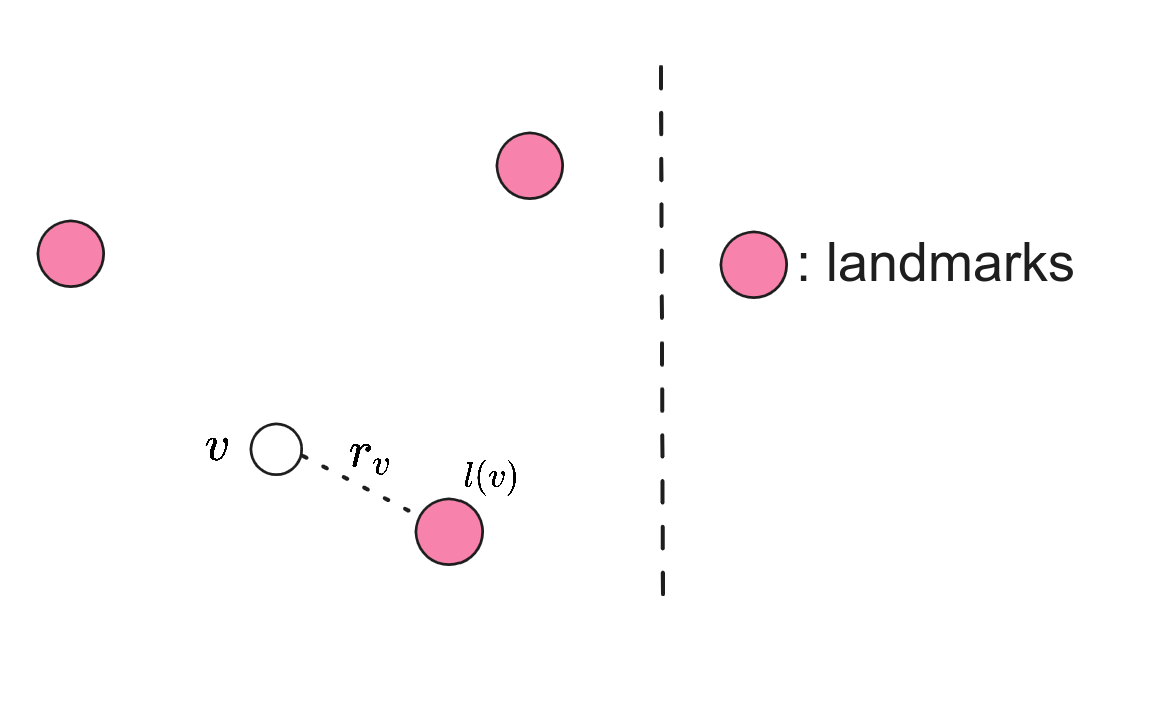
若选定了 landmark 集 $L$，则对于任意一点 $v\in V$：

$l(v)$：距离 $v$ 最近的 $L$ 中顶点；$r_v$：$v$ 和 $l(v)$ 之间的距离。

基础定义

$B(v)$：所有到 $v$ 距离小于 $r(v)$ 的点的集合。

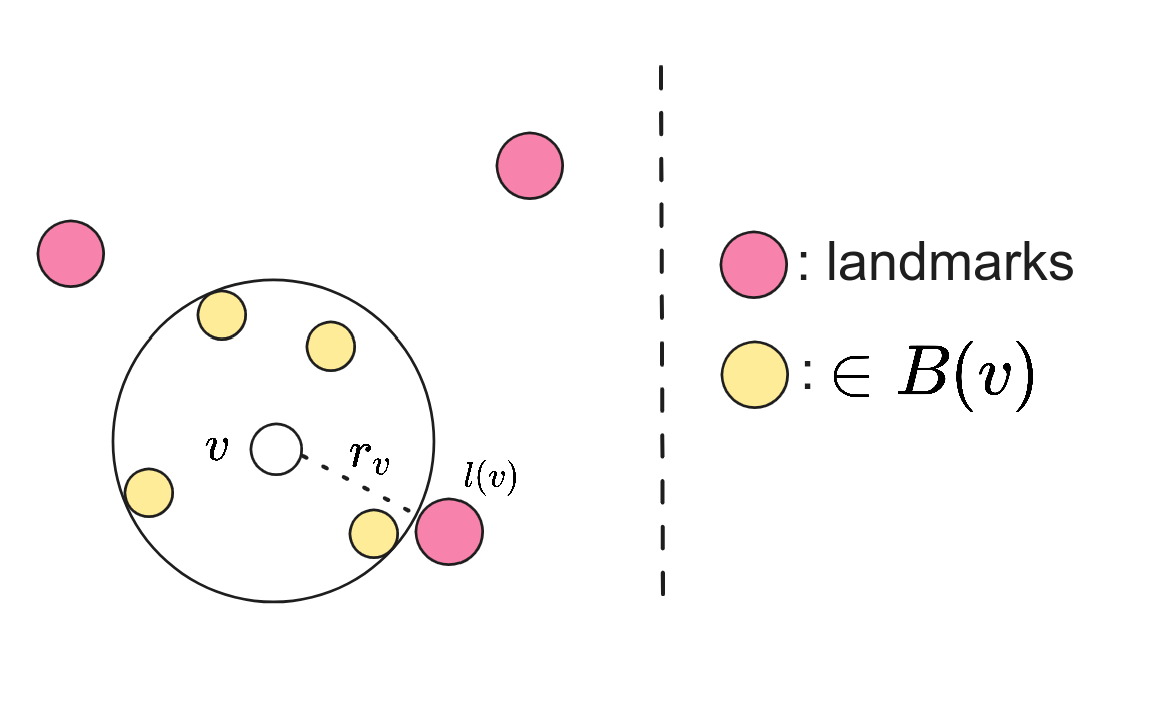
基础定义

$B^*(v)$：在 $B(v)$ 中或与 $B(v)$ 中顶点相邻的点的集合。

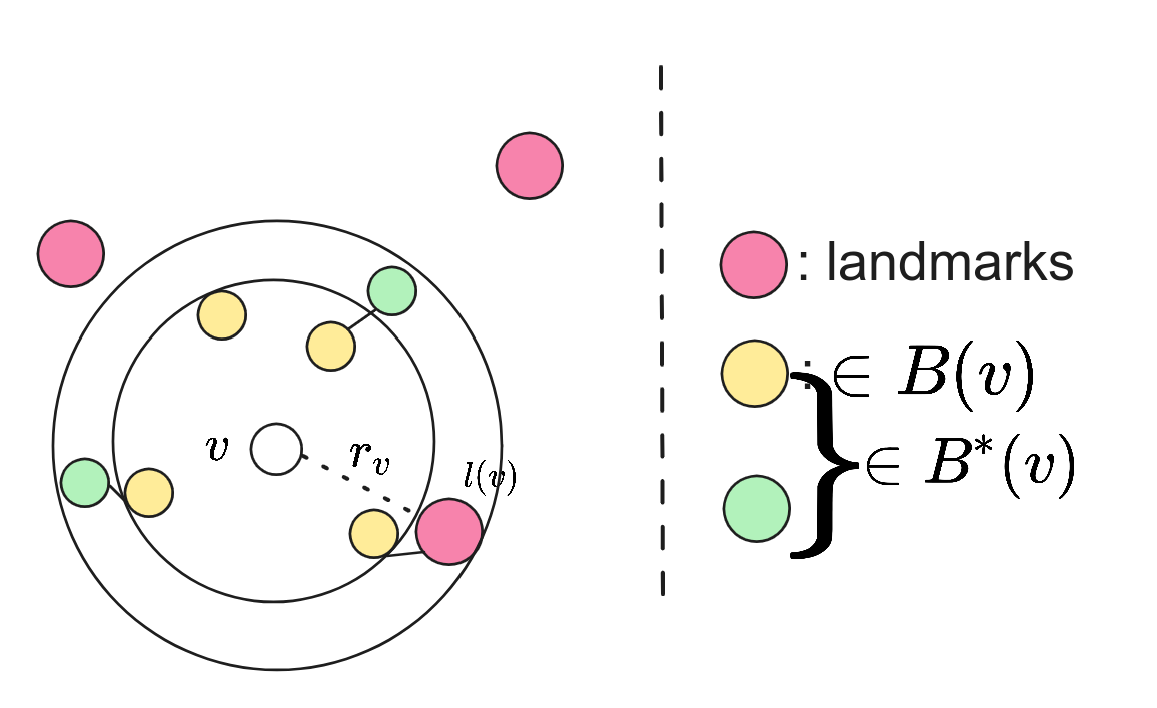
基础定义

迭代定义：

$$ \Gamma_i^*(v)=\bigcup_{w\in \Gamma^*_{i-1}(v)} B^*(w) $$

$$ \Gamma_i(v)=\bigcup_{w\in \Gamma^*_{i-1}(v)} B(w) $$

且 $\Gamma_0^*(v)=v, \Gamma_0(v)=\varnothing$.

landmark 集 $L$ 选取

Theorem: 对于最大度 $\Delta(G)=\mu$ 的图 $G$，对任意 $1\le \alpha\le n$，存在 landmark 集 $L$ 大小为 $\tilde O(n/\alpha)$，满足对任意 $v\in V$，$|B(v)|=O(\alpha)$ 从而 $|B^*(v)|=O(\alpha\mu)$, WHP。

证明：[4] (Alon & Spencer, 2016).

算法预处理

对每个点 $v$，使用一个哈希表存储到所有 $|L|=\tilde O(n/\alpha)$ 个 landmark 的距离，以及 $l(v)$ 和 $r_v$。

每个点使用 Perfect hashing，空间为 $\tilde O(n/\alpha)$。故算法总空间 $\tilde O(m+n^2/\alpha)$。

算法主过程

对于 $s$ 和 $t$ 的查询，分为三部分。

(Candidate distance 意为，只从 e.g. $\Gamma_k^*(s)$ 内部更新的距离)

$s$ 到 $t$ 的最短路

在 $s$ 到 $t$ 的最短路中，我们考虑 $\Gamma^*_i$ 的递归表现：

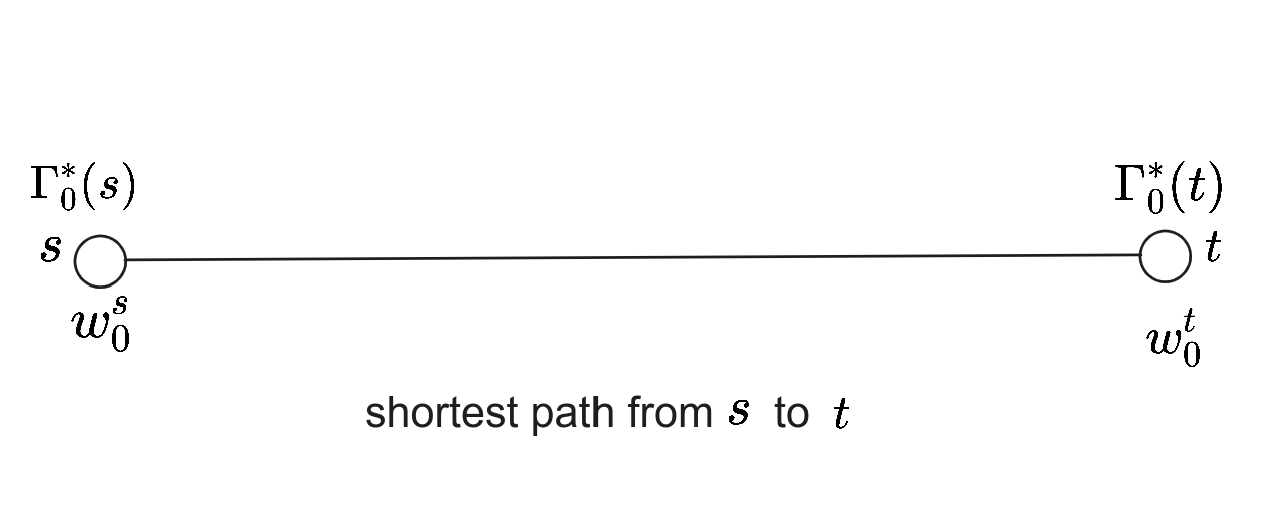
$s$ 到 $t$ 的最短路

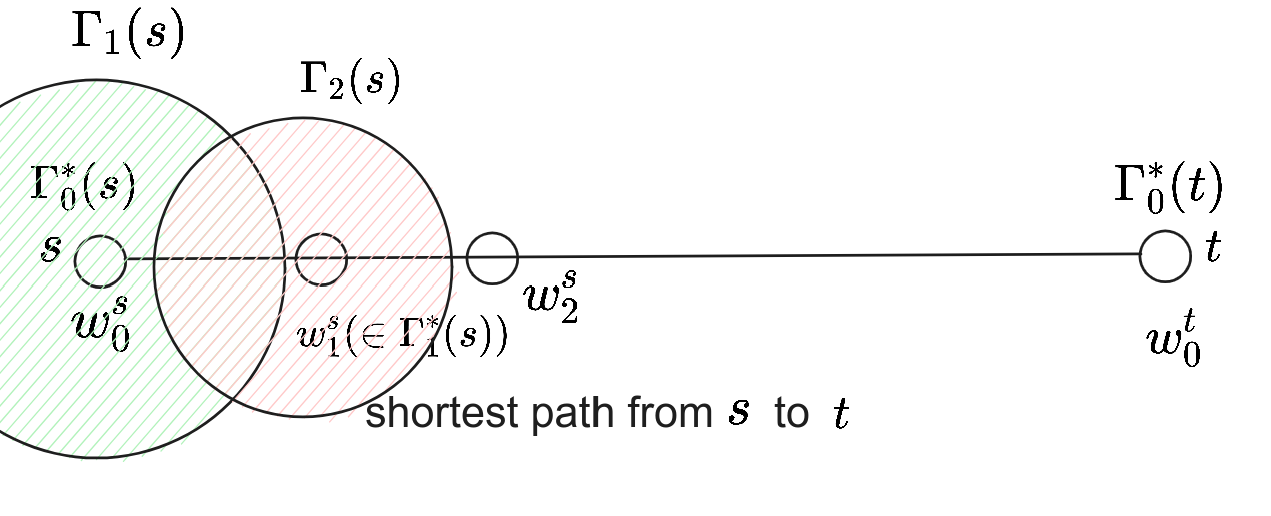
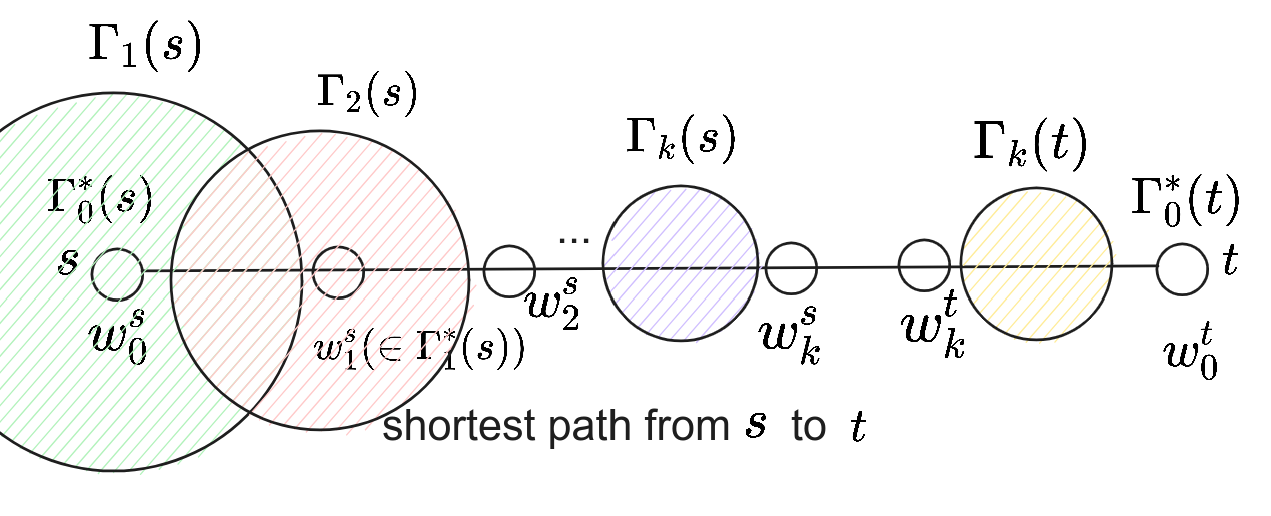
一些性质

以下性质对于 $s$ 和 $t$ 是对称的，故只证 $s$.

Property 1. 在 Query 的 1.2. 行后，可以得出所有 $s$ 到 $w_j^s(0\le j\le k)$ 的距离，也就是求得的 Candidate distance。

Property 2. 设 $r^s$ 是 $\min_{0\le j<k}r_{w^s_j}$，则 $d(s, w_i^s)\ge i\cdot r^s$。

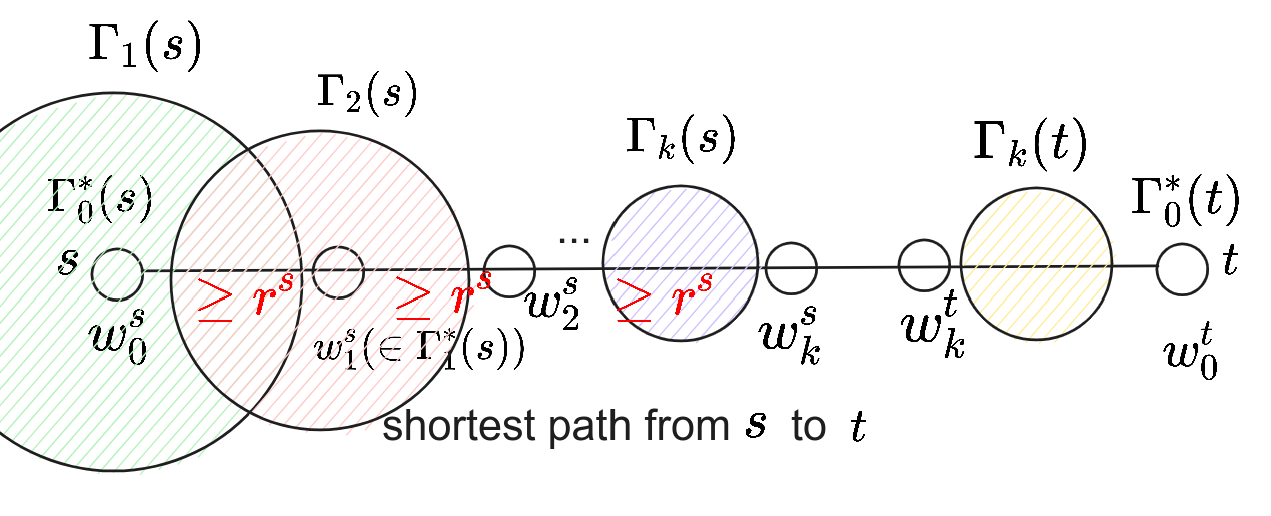
Property 3. 若 $w_k^t\notin \Gamma^*_k(s)$（即两向的迭代不交），则 $d(s, t)\ge 2k\min\lbrace r^s, r^t\rbrace$.

一些性质

Property 4. query 算法得到的估计距离 $\delta(s, t)\le d(s, t)+2\min\lbrace r^s, r^t\rbrace$.

• 这是因为第 5. 行使用更新的 $d'_s(w)+d(w, l(w))+d(l(w), t)\le d(s, t)+2r^s$。

  其中 $w$ 选择使得 $r_{w^s_j}$ 取得 $r^s$ 的 $w^s_j$。

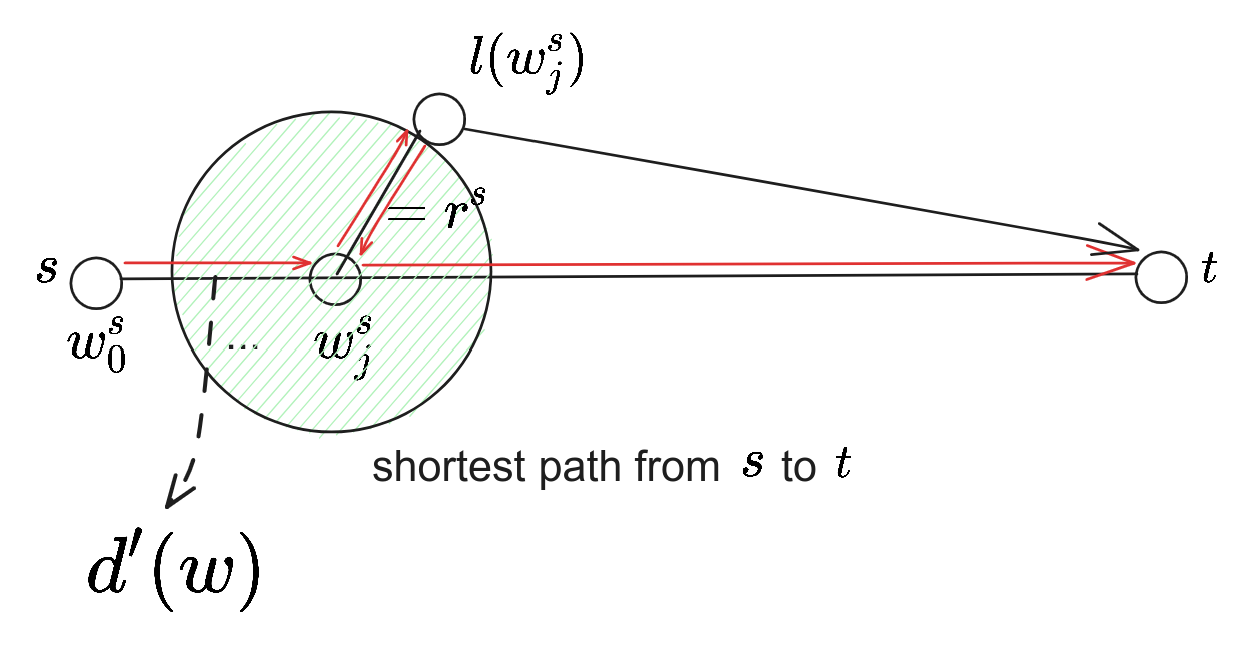
stretch 分析

1. 当 $w_k^t\in \Gamma_k^*(s)$ 时，可以得到 $\delta(s, t)=d(s, t)$，此时得到准确值。
2. 当 $w_k^t\notin \Gamma_k^*(s)$ 时，由 Property 3. 有 $d(s, t)\ge 2k\min\lbrace r^s, r^t\rbrace$；由 Property 4. 有 $\delta(s, t)\le d(s, t)+2\min\lbrace r^s, r^t\rbrace$。从而

$$ \delta(s, t)\le d(s, t)+2\min\lbrace r^s, r^t\rbrace \le d(s, t)+2\cdot d(s, t)/(2k). $$

进而

$$ \dfrac{\delta(s, t)}{d(s, t)}\le 1+1/k. $$

即 stretch 为 $1+1/k$.

由上知，该算法空间为 $\tilde O(m+n^2/\alpha)$。由于每次 query 要进行 $O(|\Gamma^*_k|)$ 范围的计算 Cadidate distance 和枚举，而每个点 $v$ 的 $|B^*(v)|=O(\alpha\mu)$，故最终单次询问复杂度为 $O((\alpha\mu)^k)$.

概述

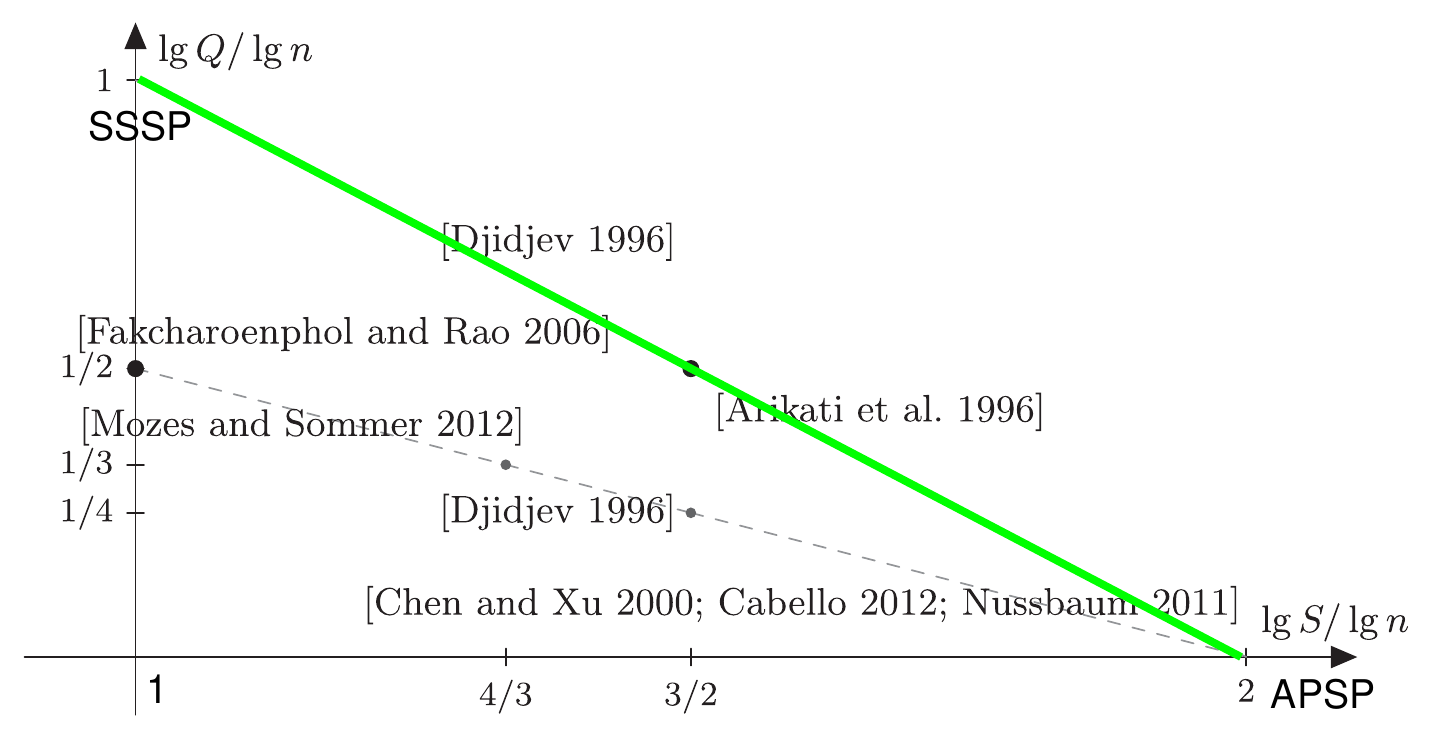
[3] (Djidjev, 1996) 给出了平面图（确切地说，$O(\sqrt n)$ 分离图）上的一种预处理时间 $O(S)$, 空间 $S=O(S)$, 单次询问时间 $T=O(n^2/S)$ 的 DO。

满足约束

$$ S\times T=O(n^2). $$

以下只展示 $S=O(n\sqrt n)$，$T=O(\sqrt n)$ 的构建方法，其余范围是它的推论。

$f(n)$ 分离性

称一类图 $\mathcal G_{f(n)}$ 具有 $f(n)$ 分离性，即对 $G\in \mathcal G_{f(n)}$，存在大小为 $O(f(n))$ 的 $C$，使得 $G-C$ 的每个连通分支的大小均不超过 $\alpha n$，其中 $\alpha<1$ 为常数。

Theorem(平面分离定理): 平面图 $\subseteq \mathcal G_{\sqrt n}$。

预处理

通过递归构造 $O(\sqrt n)$ seperator，形成一棵 $O(\log n)$ 深度的树。

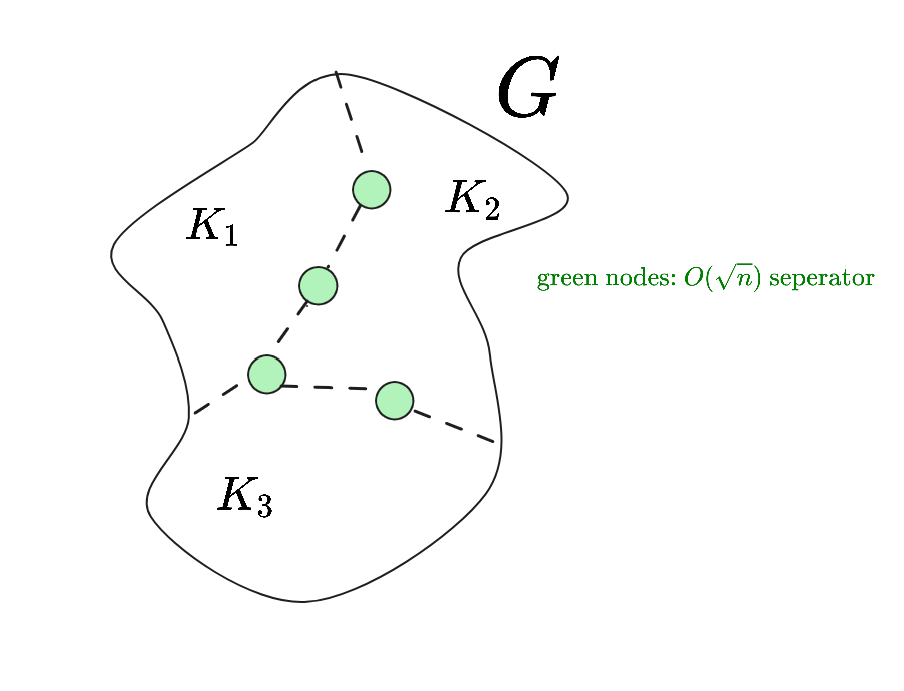
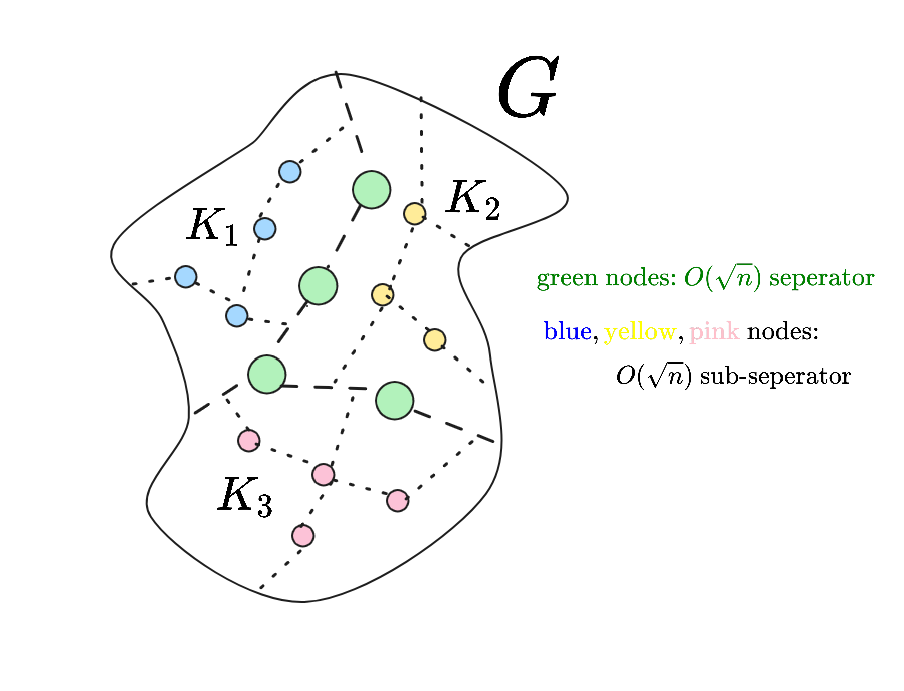
预处理

转化为树，树中的每个顶点代表原图中一个 $O(\sqrt n)$ seperator，即为：

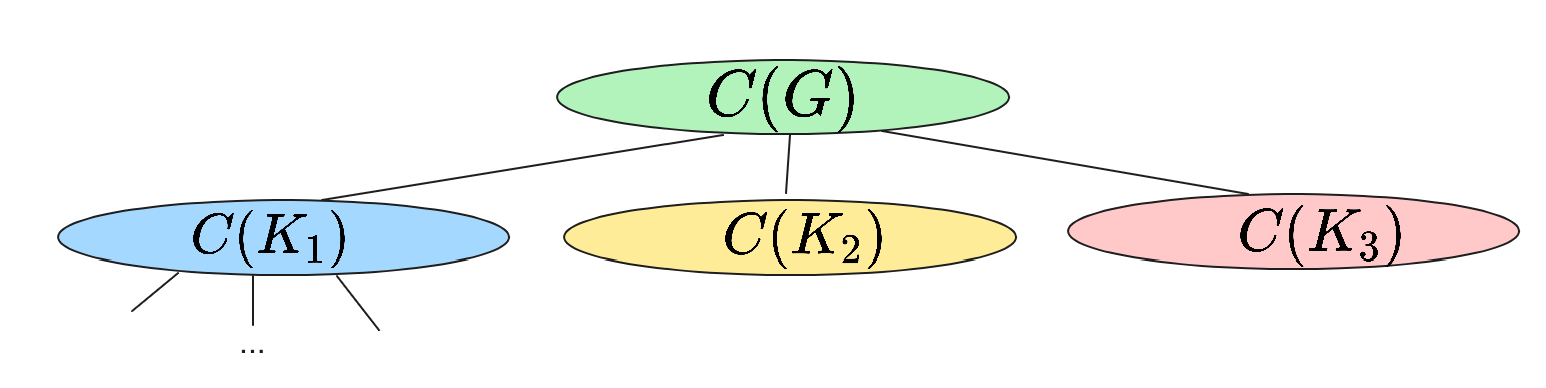
树中每个顶点即一个 $O(\sqrt n)$ seperator $C(G_x)$）代表的原图中每个顶点计算到 $G_x$ 中的每个顶点的距离）。

预处理分析

• 使用 [5] (Henzinger et.al, 1997) 的方法可以在平面图中 $O(|G|)$ 进行 SSSP。
• 计算一个大小为 $n_x$ 的$C(G_x)$ 的信息需要 $O(n_x\sqrt {n_x})$ 的预处理时间和算法总空间。

预处理时间/算法总空间共计

$$ f(n)=\sum_{i}f(n_i)+O(n\sqrt {n}), \text{where } \sum_{i}n_i=n, n_i\le \alpha n. $$

解得 $f(n)=O(n\sqrt n)$。故预处理时间，空间均为 $O(n\sqrt n)$。

询问

对于 $u, v$，找到在树中它们所在的顶点，设它们的 LCA 为 $C(G_l)$。输出答案为

$$ d(u, v)=\min_{x\in C(G_l)} \lbrace d(u, x) + d(x, v)\rbrace. $$

这是因为 $C(G_l)$ 中一定有顶点在 $u, v$ 的最短路上（它是割集）。单次询问时间 $O(\sqrt n)$。

参考文献

[1] Sommer, C. (2014). Shortest-path queries in static networks. ACM Computing Surveys (CSUR), 46(4), 1-31.

[2] Agarwal, R. (2014). The space-stretch-time tradeoff in distance oracles. In Algorithms-ESA 2014: 22th Annual European Symposium, Wroclaw, Poland, September 8-10, 2014. Proceedings 21 (pp. 49-60). Springer Berlin Heidelberg.

[3] Djidjev, H. N. (1996, June). Efficient algorithms for shortest path queries in planar digraphs. In International Workshop on Graph-Theoretic Concepts in Computer Science (pp. 151-165). Berlin, Heidelberg: Springer Berlin Heidelberg.

参考文献

[4] Alon, N., & Spencer, J. H. (2016). The probabilistic method. John Wiley & Sons.

[5] Henzinger, M. R., Klein, P., Rao, S., & Subramanian, S. (1997). Faster shortest-path algorithms for planar graphs. journal of computer and system sciences, 55(1), 3-23.